Atoms for Peace

---

Trinity

How much energy did the first "gadget" release? The following is a popular case where dimensional analysis provides a strong estimate for a measurement that would be otherwise impossible.

• The exact energy yield is probably unknown, but DoD has released estimates.

First demonstrated by G.I. Taylor, we can use dimensional analysis to obtain the approximate energy of any spherical blast, provided we have the following:

• Spatial scale of the blast as it evolves, and
• Time scale of the blast as it evolves.

We also have knowledge that:

• The blast will expand spherically (approxiamtely),
• The blast occurs in air, which is a medium we know much about.

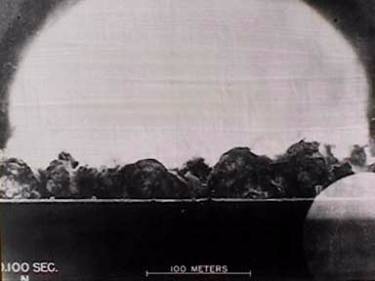
Fig. 1 - Historical photos of Trinity. Shows the evolution of blast radius over space and time. Can determine radius precisely using tracker software.

We can define the dimensional system parameters that will contribute to our blast energy $E_T$. Variables should correspond to each of our bullet points:

• $R$ = Radius of the blast.
• $E_T$ = Total energy released by the blast.
• $t$ = Time elapsed since the blast began.
• $\rho_{air}$ = Density of the medium which the blast expands into (fluid dynamics).

Where C is some dimensionless constant that we cannot determine using dimensional analysis, our relationship is given by the following product:

$$E_T = C R^{\alpha} \rho^{\beta} t^{\gamma} \tag{1.1}$$ This produces a system of equations for $\alpha, \beta, \gamma$ that is easy to solve using linear algebra: $$ \begin{align}[E_T] = M^1 L^2 T^{-2} &= L^{\alpha} (M L^{-3})^{\beta} T^{\gamma} \\ M^1 L^2 T^{-2} &= M^{\beta} L^{(\alpha -3 \beta)} T^{\gamma} \end{align} \tag{1.2} $$ $$ $$ \begin{cases} 0 \alpha + 1 \beta + 0 \gamma = 1 \\ 1 \alpha -3 \beta + 0 \gamma= 2 \\ 0 \alpha + 0 \beta + 1 \gamma = -2 \end{cases}$$ $$ $$ \begin{bmatrix} 0 & 1 & 0 & 0\\ 1 & -3 & 0 & 2\\ 0 & 0 & 1 & -2 \end{bmatrix} \stackrel{rr}{ \rightarrow} \begin{bmatrix} 1 & 0 & 0 & 5\\ 0 & 1 & 0 & 1\\ 0 & 0 & 1 & -2 \end{bmatrix} \tag {1.3}$$ $$\blbox{E_T(t) = \frac{C R^5 \rho}{t^2}} \tag{1.4} $$

---

Energy Released by Trinity

Experimental determinations (from Taylor) cite $C \approx 1.036$, so this gives us energy values of: \begin{matrix} E_1 & \approx & 8.85*10^{13} J\\ E_2 & \approx & 5.64*10^{13} J\\ E_3 & \approx & 4.73*10^{13} J\\ E_4 & \approx & 2.73*10^{13} J\\ \end{matrix}

Table 1 - Any variance in $E$ is due to error. We can break this variance down statistically to show that our estimations are actually pretty precise.

The average of these values gives our best approximation of Trinity's energy-yield: $$\bar{E}_T = 5.8*10^{13}\ \text{Joules}$$ $$\blbox{\bar{E}_T \approx 13.9 \ \text{Kiloton of TNT} }\tag{1.5}$$

Energy measurements of this blast were around 18.9 Kilotons according to the DoD [Needs Citation], making this a decent approximation given our limited information.

Why is an error of 26% considered good? The only measurements we took from the blast are time (s) and distance (m). We know nothing about the materials used in the blast; no understanding of its chemistry or engineer. Most of us know nothing about the energy released by any kind of blast. If we took the same information and inferred the energy released, the order of magnitude would be a complete guess. 10KJ? 100*10^25J? How much energy does a "regular" blast even release?

---

So my country's purpose is to help us to move out of the dark chamber of horrors into the light... forward towards peace and happiness and well-being.

   -Atoms for Peace, December 1953