Home Page

Next Page

• Set theory provides resolution to paradoxes in our real number system, and allows us to define various number systems and operations with mathematical rigor.
• Extending our number system from the naturals through to the reals ($\Bbb{N} \subseteq \Bbb{Z} \subseteq \Bbb{Q} \subseteq \Bbb{R}$) is required if every length along the number line is to correspond to a value that we can actually define (Abbott, 2000 pg. 4). This seems like a requirement of the standard model, where spacetime is taken as continuous.
• Functions may be generalized to a definition which is far less restrictive than the criteria proposed during introductory courses in algebra and single-variable calculus. This is necessary when special functions (distributions) which appear in abundance in physics -- like Heaviside and Dirac-delta.

---

The Holes in our Rational Number Line

Consider this bizarre function proposed by Dirichlet:

$$ f(x) = \begin{cases} 1\ \ \text{if} \ x \in \Bbb{Q} \\ 0\ \ \text{if} \ x \notin \Bbb{Q} \end{cases} \tag{Eq. 1}$$

Plotting this function produces a figure that is highly discontinuous. As a result, f(x) pushes notions of being single-valued by appearing to produce two horizontal lines using inputs of x.

Resolution will not affect the plot's fine-structure or 'smoothness'. The Archimedean Property, held by rationals and reals, guarantees that there are infinite irrationals between any two elememts of $\Bbb{Q}$, fitting this observation.

Fig 1. - A plot of f(x). This is a single function, coded numerically in MATLAB; this is not a plot of two functions stacked on top of one another.

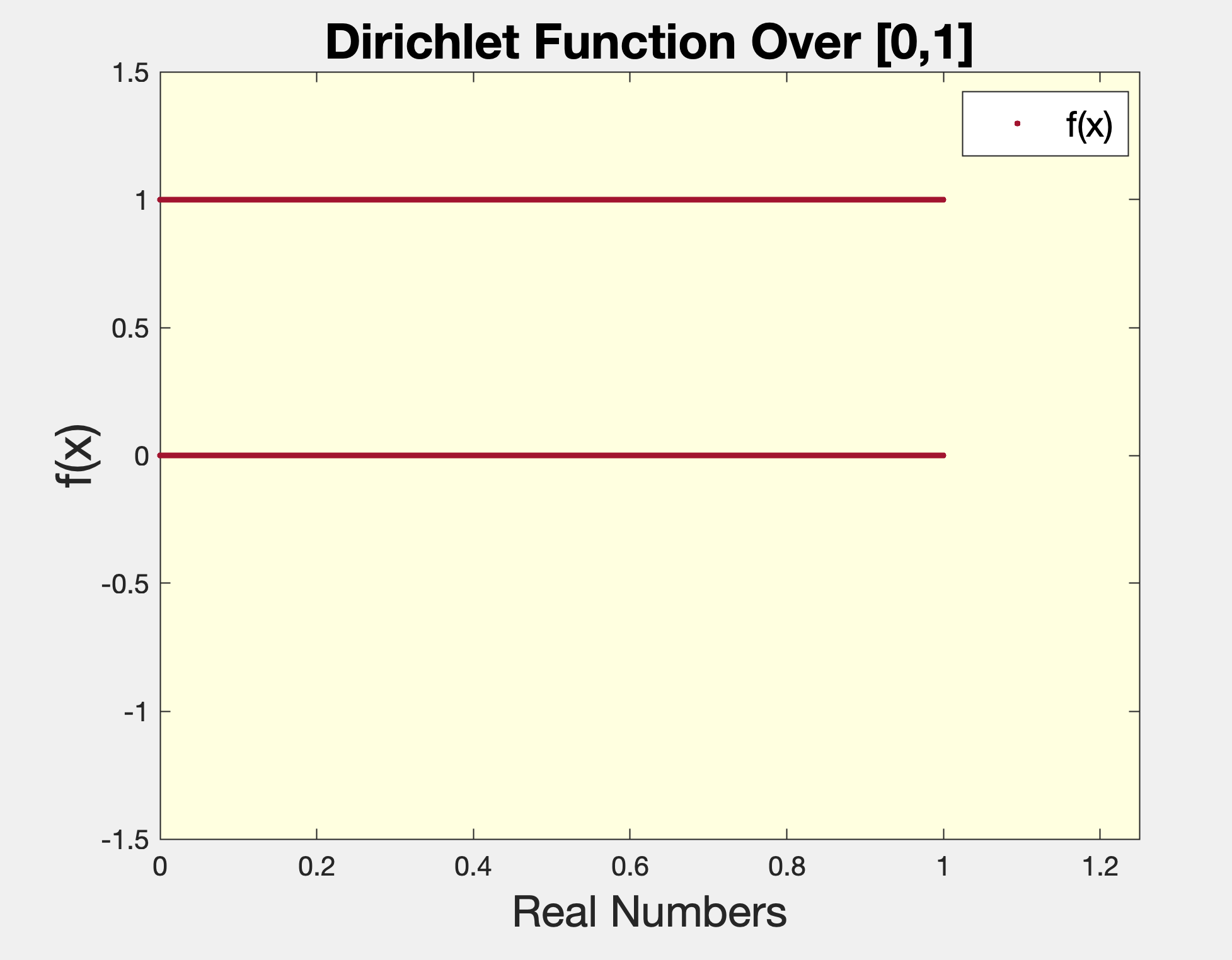
Here are some important observations about $f(x)$:

• The irrational number line (situated at $f(x)=0$) is constructed from the "holes" in the rational number line above it (at $f(x)=1$).

• On a macroscopic scale, this demonstrates that elements of $\Bbb{Q}$ are dense in $\Bbb{R}$.

• Paradoxically, both sets of points consist of infinitely-many elements.

This property of $\Bbb{Q}$ to appear continuous, regardless of domain scope, is why the rational numbers form a field and support the identities for multiplication, division, addition and subtraction. For example, every element of $\Bbb{Z}$ has the multiplication inverses to support division.

---

Providing Visualization for $\Bbb{Q}$'s Unique Density in $\Bbb{R}$

An interesting way to show that $\Bbb{Q}$ has density, as opposed to its subsets $\Bbb{N}$ and $\Bbb{Z}$, is to plot an analogue to Dirichlet's function, but with integers at $f(x)=1$ and $x \in \Bbb{Q} \land x \notin \Bbb{Z}$ at f(x)=0. In this case, the empty intervals between the upper set of points ($\Bbb{Z}$) will be filled by the rationals of $\Bbb{Q}$ -- analogous to (Fig. 1) where the holes of $\Bbb{Q}$ were filled by the irrationals:

$$ f_{\Bbb{Z}}(x) = \begin{cases} 1\ \ \text{if} \ x \in \Bbb{Z} \\ 0\ \ \text{if} \ x \in \Bbb{Q} \land x \notin \Bbb{Z} \end{cases} \tag{Eq. 2}$$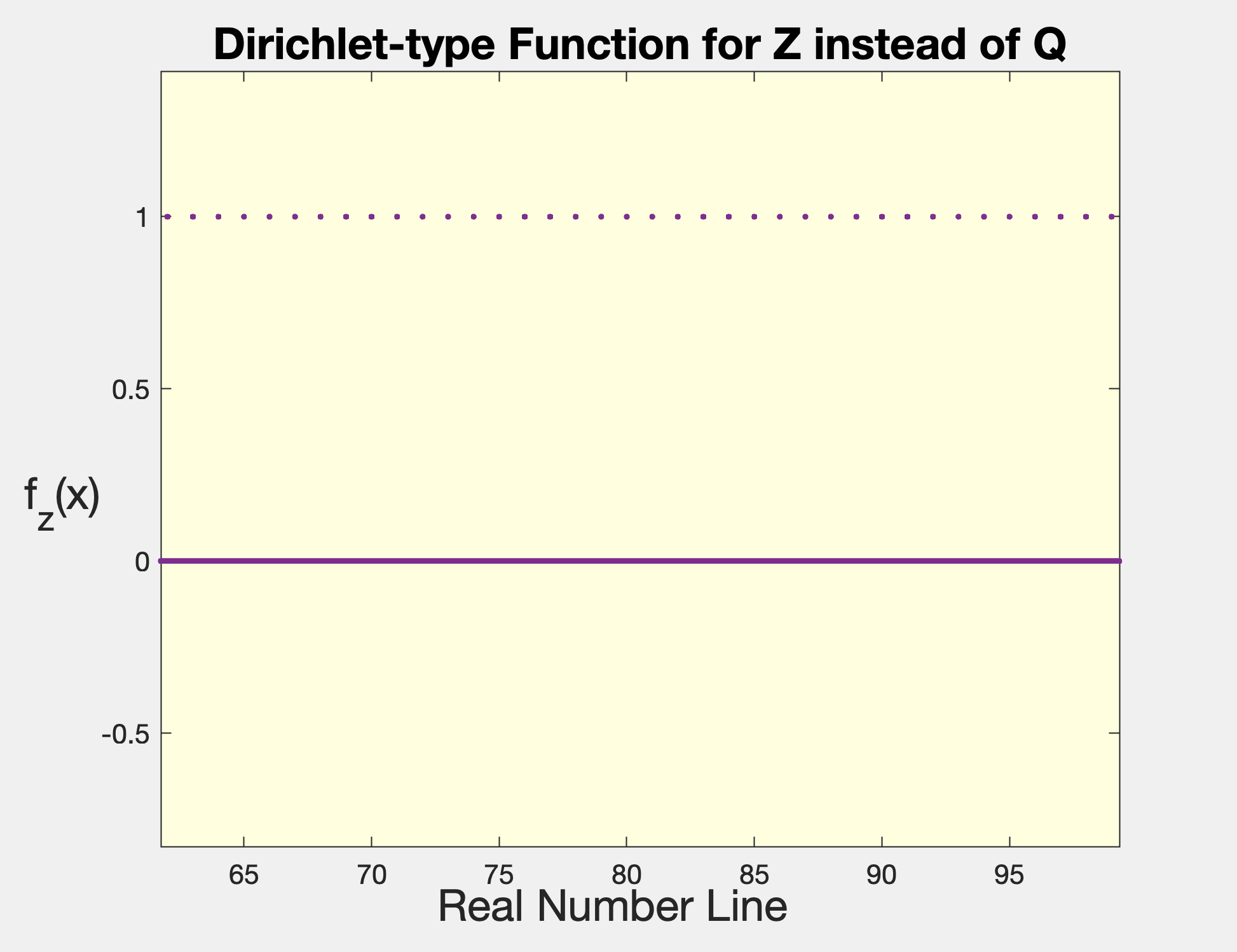 Fig 2. - A plot of $f_{\Bbb{Z}}(x)$ over a domain that demonstrates how empty intervals in $\Bbb{Z}$ are filled by densely-packed rationals.

Irrationals are absent from (Eq. 2), yet the set at $f_{\Bbb{Z}}(x)=0$ still looks continuous;

---

Boundedness of our Number System

A common approach to the real number line begins with the Axiom of Completeness and the Archimedean Property. These are leveraged to understand the rational set ($\Bbb{R}$), infinities, boundedness, and dense sets.

• Axiom of Completeness: Every nonempty set of real numbers that is bounded above has a least upper bound (Abbott, 2000, p.14).
• Archimedian Property (i): Given any number $x \in \Bbb{R}$, there exists an $n \in \Bbb{N}$ satisfying $n \gt x$
  
• Archimedian Property (ii): Given any number $y \in \Bbb{R}$, there exists an $n \in \Bbb{N}$ satisfying $1/n \lt y$
  (Abbott, 2000, p.19)

---

Taking a surface-level look at our own number system through the context of these statements, familiar concepts fall out of [semi-]rigorous foundation:

• The natural numbers set $\Bbb{N}$ leads with 1, and thus is bounded below (infinum 1). It is not bounded above. Absence of an upper-bound fits with layman notions for the infinite: the natural set begins but it never ends.

$$\Bbb{N} = \{1,2,3,4,\dots \}$$

• The integer set $\Bbb{Z}$ is not bounded above, but unlike $\Bbb{N}$ it is neither bounded below. However, like $\Bbb{N}$ its elements are ordered and countably infinite.

$$\Bbb{Z} = \{ \dots , -2, -1, 0, 1, 2, \dots \}$$

• The rational field $\Bbb{Q}$ contains the set $\Bbb{Z}$. Therefore, $\Bbb{Q}$ will not be bounded below or above, yet it is still ordered and countably infinite.

$$\Bbb{Q} = \{ p/q : p \land q \in \Bbb{Z},\ q \notin 0 \}$$
Defining $\Bbb{Q}$ requires "more" notation than its subsets. Despite being countably infinite like the naturals and the integers, it is impossible to list adjacent elements in the rational number set.

---

Applying this concept elsewhere, consider some set $A$ with elements that are ordered as such:

$$ A = \{r^2 \gt 2\ :\ x \in \Bbb{Q}\} \tag{Eq. 3} $$

Set $A$ contains all rational numbers $r^2$ that are greater than 2, not including 2 itself.

• Rational numbers form an ordered set (field) that is countable, and set A contains all rationals greater than 2
• Therefore, set A is also ordered and countable; these properties are inherited from $\Bbb{Q}$.
• A must be bounded below with a greatest lower bound (infinum) of 2, despite $2 \notin A$.

$$ \bbox[8px,border:1px solid black]{ \text{inf} A=2} $$

---